Question

A simple watermelon launcher is designed as a spring with a light platform for the watermelon. When an 8.00 kg watermelon is put on the launcher, the launcher spring compresses by 10.0 cm. The watermelon is then pushed down by an additional 30.0 cm and it’s ready to go. Just before the launch, how much energy is stored in the spring?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Force from Hooke's law, the force since Newton's second law and the potential elastic energy.

Since the forces are balanced the Spring force is equal to the force of the weight that is

`F_s = F_g`

`kx = mg`

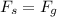
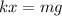
Where,

k = Spring constant

x = Displacement

m = Mass

g = Gravitational Acceleration

Re-arrange to find the spring constant

`k = (mg)/(x)`

`k = (8*9.8)/(0.1)`

`k = 784N/m`

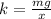
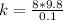
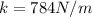
Just before launch the compression is 40cm, then from Potential Elastic Energy definition

`PE = (1)/(2) kx^2`

`PE =(1)/(2) 784*0.4^2`

`PE = 63.72J`

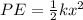
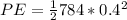
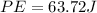
Therefore the energy stored in the spring is 63.72J