Question

A 2150 kg car, moving East at 10 m/s, collided and joins with a 3250 kg car. The cars move East together at 5.22 m/s. What is the 3250 kg car's initial velocity calculated to the nearest tenth?

Answer 1

The second car was moving at 2.1 m/s to the east

Step-by-step explanation:

Conservation Of Linear Momentum

The total momentum of a system of bodies is constant if no external force is applied to it. The momentum of a body with mass m and velocity v is p=mv. When two objects collide and join together afterward, the total mass is the sum of the individual masses, and the final speed is common to both.

Let's say

`\displaystyle m_1,\ m_2\ ,\ v_1,\ v_2\ ,\ p_1,\ p_2`

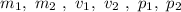
are the masses of the objects 1 and 2, their speeds, and their linear momentums respectively before the collision, and

`\displaystyle v_1',\ v_2'\ ,\ p_1',\ p_2'`

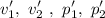
are the speeds of each object and their linear momentums after the collision.

The principle of conservation of linear momentum states that

`\displaystyle p_1+p_2=p_1'+p_2'`

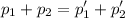
This means that

`\displaystyle m_1\ v_1+m_2\ v_2=m_1\ v_1'+m_2\ v_2'`

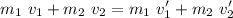
Since both cars remain together after the collision,

`\displaystyle v_1'=v_2'=v'`

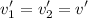
The relation becomes

`\displaystyle m_1\ v_1+m_2\ v_2=(m_1+m_2)\ v'`

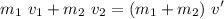
Solving for
`v_2`

`\displaystyle v_2=((m_1+m_2)v'-m_1\ v_1)/(m_2)`

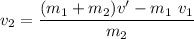
The given data is

`\displaystyle m_1=2150\ kg\ ,\ m_2=3250\ kg\ ,\ v_y=10\ m/s,\ v'=5.22\ m/s`

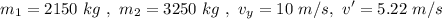
Let's assume all the speeds are positive towards East

Replacing those values

`\displaystyle v_2=((2150+3250)5.22-2150(10))/(3250)`

`\displaystyle v_2=(6688)/(3250)=2.06\ m/s`

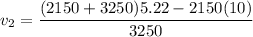
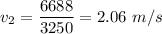
The second car was moving at 2.1 m/s (to the nearest tenth) to the east