Question

The height of a toy rocket that is shot in the air with an upward velocity of 48 feet per second can be modeled by the function , where t is the time in seconds since the rocket was shot and f(t) is the rocket’s height in feet. What is the maximum height the rocket reaches?

Answer 1

Answer: 36!!!

Explanation:

Answer 2

maximum height reached = 35 feet

and
`f(t) = 48t-16.07t^(2)`

Explanation:

writing linear motion equations

`s = ut + (1)/(2)at^(2)`

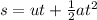
where s is the total displacement, u the initial velocity, t the time travelled, and a is the acceleration.

given u = 48 ft/s, and a = acceleration due to gravity g = -9.8
`(m)/(s^(2))`

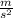
1 m = 3.28 feet therefore g becomes -9.8×3.28
`(ft)/(s^(2))`

here negative sigh comes as acceleration due to gravity is in opposite direction of initial velocity.

therefore f(t) becomes
`f(t) = 48t-16.07t^(2)`

to find max height we should find differentiation of f(t) and equate it to 0

therefore we get 48 = 32.144t

t = 1.49 s

therefore max height f(1.49) = 71.67-36.67 = 35 feet