Answer:
The solution is x=3, y=1
Explanation:
we have
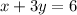 ----> equation A
----> equation A
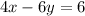 ----> equation B
----> equation B
Rewrite each equation in slope intercept form

Equation A
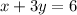
isolate the variable y
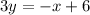
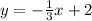 ----> equation A in slope intercept form
----> equation A in slope intercept form
Equation B
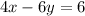
isolate the variable y
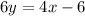
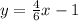
Simplify
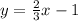 ----> equation B in slope intercept form
----> equation B in slope intercept form
Solve the system by graphing
Remember that the solution of the system of equations is the intersection point both graphs
using a graphing tool
The intersection point is (3,1)
therefore
The solution is x=3, y=1
see the attached figure