Question

1) Members at a yoga school pay $10 per class plus a one-time $100 membership fee. Non-members pay$15 per class. How many classes would a member have to take to save money compared to taking classes as a non-member?

2) Translate the statement into an equation. Then solve the equation. The sum of 8 and 3 times a number is 23.

6) Members at a yoga school pay $7 per class plus a one-time $120 membership fee. Non-members pay $11 per class. How many classes would a member have to take to save money compared to taking classes as a non-member?

Answer all questions please, and if u can show u work, please...

3)A rental car costs $36 for one day plus an additional $0.42 per mile. What is the cost of renting a car for one day and driving it 78 miles?

4) Alice earns 1.5 times her normal hourly rate for each hour she works after 40 hours in a week. She worked 50 hours this week and earned $660. What is her normal hourly rate?

5) Cynthia orders 27 prints of a photograph she took. It costs her a total of $242.73. Which equation can be used to find how much each print cost?

Answer 1

Part 1) The number of classes must be greater than 20

Part 2) see the explanation

Part 3)
`\$68.76`

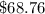
Part 4)
`\$12\ per\ hour`

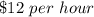
Part 5) The equation that can be used is
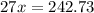`27x=242.73` and the cost of one print is
`\$8.99`

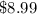
Part 6) The number of classes must be greater than 30

Explanation:

Part 1) we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the slope or unit rate

b is the y-intercept or initial value

Let

y ----> the total cost

x ----> the number of classes

we have

Members

The slope is
`m=\$10\ per\ class`

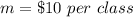
The y-intercept is
`b=\$100`

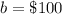
so

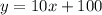`y=10x+100` ----> equation A

Non-Members

The slope is
`m=\$15\ per\ class`

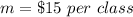
so

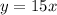`y=15x` ----> equation B

To find out how many classes would a member have to take to save money compared to taking classes as a non-member, solve the following inequality

`10x+100 < 15x`

Solve for x

subtract 10 x both sides

`100 < 15x-10x`

`100 < 5x`

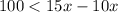
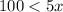
Divide by 5 both sides

`20 < x`

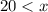
Rewrite

`x > 20`

therefore

The number of classes must be greater than 20

Part 2) we have

The sum of 8 and 3 times a number is 23.

Let

x ----> the number

Remember that

3 times a number is the same that multiply 3 by the number ----> 3x

so

The sum of 8 and 3 times a number is 23 is the same that

`8+3x=23`

solve for x

subtract 8 both sides

`3x=23-8`

`3x=15`

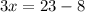
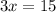
Divide by 3 both sides

`x=5`

Part 3) we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the slope or unit rate

b is the y-intercept or initial value

Let

y ----> the total cost of renting a car for one day

x ----> the number of miles

we have

The slope is
`m=\$0.42\ per\ mile`

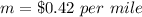
The y-intercept is
`b=\$36`

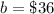
so

`y=0.42x+36`

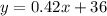
For x=78 miles

substitute in the linear equation and solve for y

`y=0.42(78)+36`

`y=\$68.76`

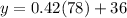
Part 4) Let

x ----> Alice's normal hourly rate

we know that

40 hours multiplied by her normal hourly rate plus 10 hours (50 h-40 h) multiplied by 1.5 times her normal hourly rate must be equal to $660

so

The linear equation that represent this situation is

`40x+10(1.5x)=660`

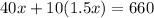
solve for x

`40x+15x=660`

`55x=660`

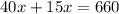
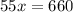
Divide by 55 both sides

`x=\$12\ per\ hour`

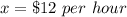
Part 5) Let

x ----> the cost of one print

we know that

The cost of one print multiplied by 27 prints must be equal to $242.73

so

The linear equation is equal to

`27x=242.73`

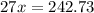
solve for x

Divide by 27 both sides

`x=\$8.99`

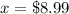
Part 6) we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the slope or unit rate

b is the y-intercept or initial value

Let

y ----> the total cost

x ----> the number of classes

we have

Members

The slope is
`m=\$7\ per\ class`

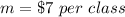
The y-intercept is
`b=\$120`

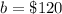
so

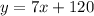`y=7x+120` ----> equation A

Non-Members

The slope is
`m=\$11\ per\ class`

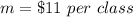
so

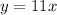`y=11x` ----> equation B

To find out how many classes would a member have to take to save money compared to taking classes as a non-member, solve the following inequality

`7x+120 < 11x`

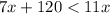
Solve for x

subtract 7x both sides

`120 < 11x-7x`

`120 < 4x`

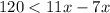
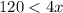
Divide by 4 both sides

`30 < x`

Rewrite

`x > 30`

therefore

The number of classes must be greater than 30