Answer:
3. What is the probability that an adult selected at random has both a landline and a cell phone?
A. 0.58
4. Given an adult has a cell phone, what is the probability he does not have a landline?
C. 0.3012
Explanation:
We solve this problem building the Venn's diagram of these probabilities.
I am going to say that:
A is the probability that an adult has a landline at his residence.
B is the probability that an adult has a cell phone.
C is the probability that a mean is neither of those.
We have that:
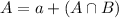
In which a is the probability that an adult has a landline but not a cell phone and
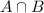 is the probability that an adult has both of these things.
is the probability that an adult has both of these things.
By the same logic, we have that:
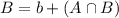
The sum of all the subsets is 1:
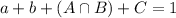
2% of adults have neither a cell phone nor a landline.
This means that
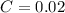 .
.
73% of adults have a landline at their residence (event A); 83% have a cell phone (event B)
So
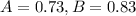 .
.
What is the probability that an adult selected at random has both a landline and a cell phone?
This is
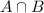 .
.
We have that
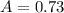 . So
. So
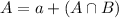
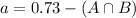
By the same logic, we have that:
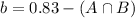 .
.
So
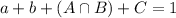
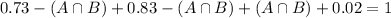

So the answer for question 3 is A.
4. Given an adult has a cell phone, what is the probability he does not have a landline?
83% of the adults have a cellphone.
We have that
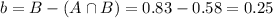
25% of those do not have a landline.
So
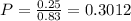
The answer for question 4 is C.