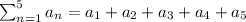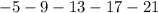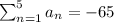Answer:
The signa notation to represent the first five ten f(x) is given by
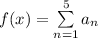
Explanation:
Given sequence is -5, -9, 13...
Let f(x) be the given sequence and is denoted by

Let the first term be
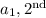 term be
term be
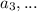
ie,
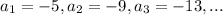
To find the common difference d:
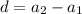

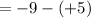
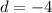
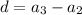


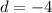
Therefore the common difference d is -4 for given sequence f(x) with
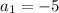 and d=-4, the seqence f(x) is an arithmetic sequence
and d=-4, the seqence f(x) is an arithmetic sequence
By defintion of arithmetic sequence

Now to find
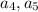 :
:
put n=4 in equation (1)
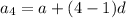
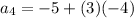 [since a=-5, d=-4]
[since a=-5, d=-4]
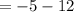
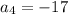
in equation (1)

 [since a=-5, d=-4]
[since a=-5, d=-4]


Therefore
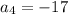 and
and

Therefore
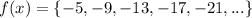
Now to represent the sum of the first five terms of f(x) using sigma notation as below
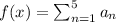
where