Answer:
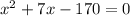
Explanation:
Here is the complete question: The width of a rectangle is 7 meters greater than its length . If the area of the rectangle is 170 m², write the quadratic equation in standard form for the equation that would represent the area of the rectangle. Let x equal to the length of the rectangle.
Given: Width of rectangle is 7 meter greater than length
Length of rectangle is x.
Area of rectangle= 170 m²
Now as given, length is x meter and width is (x+7) meter
we know that, area of rectangle=
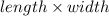
∴ substitute the values to get correction equation.
⇒170=
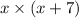
now distributing x into (x+7).
⇒
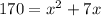
subtracting 170 both side.
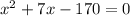
∴
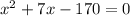 is the quadratic equation in standard form for the equation that would represent the area of the rectangle.
is the quadratic equation in standard form for the equation that would represent the area of the rectangle.