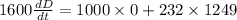Question

The pilot of a Coast Guard patrol aircraft on a search mission had just spotted a disabled fishing trawler and decided to go in for a closer look. Flying in a straight line at a constant altitude of 1000 ft and at a steady speed of 232 ft/sec, the aircraft passed directly over the trawler. How fast was the aircraft receding from the trawler when it was 1600 ft from the trawler?

Answer 1

`(dD)/(dt)= 181(168)/(1600)`

Explanation:

h= 1000 ft

dx/dt= 232 ft/sec

D= 1600 ft

First, we have to find a distance x ( shown in the figure)

applying pythagorus theorem

D^2= h^2+x^2................1

x^2= D^2-h^2

= 1600^2-1000^2

x^2= 1560000

x=1248.99 m

Now we can find out how fast the aircraft is receding from the trawler

( notice that the height is not changing)

so differentiating equation 1 w.r.t t we get

`(d)/(dt) (D^2)= (d)/(dt)(h^2+x^2)`

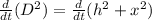
2DD'= 2hh'+2xx'

`D(dD)/(dt)= h(dh)/(dt)+x(dx)/(dt)`

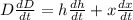
now putting values we get

`1600(dD)/(dt)= 1000*0+232*1249`

`(dD)/(dt)= 181(168)/(1600)`