Answer:
1) Option c) is correct ie., 5 real and o non-real
2) Option b) is correct ie., (4,
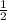 ,
,
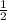 , 2,2)
, 2,2)
Explanation:
Given polynomial function is
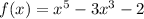
To find zeros equate f(x) to zero ie.,
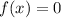
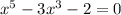
By synthetic division
| 1 0 -3 0 -2
-1 | 0 -1 1 2 2
|_________________
1 -1 -2 2 0
Therefore x=-1 is a zero

| 1 -1 -2 2
1 | 0 1 0 2
|___________________
1 0 -2 0
x=1 is the zero
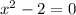
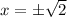
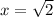 and
and
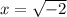
Option c) is correct ie., 5 real and o non-real
2) Given polynomial function is
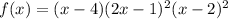
To find zeros equate f(x) to zero ie.,
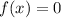
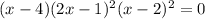
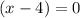 (or)
(or)
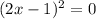 or
or
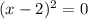
Therefore x=4,
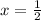 of multiplicity of 2 and x=2 multiplicity of 2
of multiplicity of 2 and x=2 multiplicity of 2
Option b) is correct ie., (4,
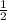 ,
,
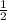 , 2,2)
, 2,2)