cost of one regular admission ticket = $ 10
cost of one senior citizen ticket = $ 5
Solution:
Let "r" be the cost of one regular admission ticket
Let "s" be the cost of one senior citizen ticket
Given that,
On day 1 you sold 30 Regular Admission tickets and 20 Senior Citizen tickets for a total of $400
So we can frame a equation as:
30 Regular Admission tickets x cost of one regular admission ticket + 20 Senior Citizen tickets x cost of one senior citizen ticket = $ 400
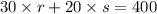
30r + 20s = 400 ----- eqn 1
Day two you sell 40 Regular Admission tickets and only 10 Senior Citizen tickets for a total of $450
So we can frame a equation as:
40 Regular Admission tickets x cost of one regular admission ticket + 10 Senior Citizen tickets x cost of one senior citizen ticket = $ 450

40r + 10s = 450 ---- eqn 2
Let us solve eqn 1 and eqn 2 to find values of "r" and "s"
Multiply eqn 2 by 2
80r + 20s = 900 --- eqn 3
Subtract eqn 1 from eqn 3
80r + 20s = 900
30r + 20s = 400
(-) ---------------------
50r = 500
r = 10
Substitute r = 10 in eqn 1
30r + 20s = 400
30(10) + 20s = 400
300 + 20s = 400
20s = 100
s = 5
Thus we have:
cost of one regular admission ticket = $ 10
cost of one senior citizen ticket = $ 5