Question

The length of the rectangle is 5 inches more than twice the length of the side of the square

Answer 1

The length of Rectangle is (5 + 2 s) inches and width of rectangle is
`(s^(2) )/(5 + 2 s)` inches .

Explanation:

Given as :

The length of the rectangle is 5 inches more than twice the length of the side of the square

The area of Rectangle = The area of square

Let the side of the square = s inches

So, The Area of square = side × side

I.e The Area of square = s × s = s² inches²

Again

Let The length of rectangle = L inches

And The width of rectangle = w inches

So, The Area of Rectangle = ( L × w ) inches²

So, According to question

The length of rectangle = 5 inches + twice length of square side

I.e L = ( 5 + 2 s ) inches

∵ Both The area same

So, L× w = s²

Or, w =
`(s^(2) )/(L)`

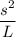
or, w =
`(s^(2) )/(5 + 2 s)` inches

So, The measure of length of Rectangle = L = (5 + 2 s) inches and width of rectangle = w =
`(s^(2) )/(5 + 2 s)` inches

Hence, The measure of length of Rectangle is (5 + 2 s) inches and width of rectangle is
`(s^(2) )/(5 + 2 s)` inches . Answer