Question

One week Beth bought 3 apples and 8 pears for 14.50. The next week she bought 6 apples and 4 pears and paid 14$ find the cost of 1 apple and 1 pear

Answer 1

Cost of 1 apple is $ 1.5 and cost of 1 pear is $ 1.25

Solution:

Let "a" be the cost of 1 apple

Let "p" be the cost of 1 pear

Given that,

One week Beth bought 3 apples and 8 pears for 14.50

So we can frame a equation as:

3 apples x cost of 1 apple + 8 pears x cost of 1 pear = 14.50

`3 * a + 8 * p = 14.50`

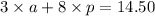
3a + 8p = 14.50 ----- eqn 1

The next week she bought 6 apples and 4 pears and paid 14$

So we can frame a equation as:

6 apples x cost of 1 apple + 4 pears x cost of 1 pear = 14

`6 * a + 4 * p = 14`

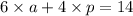
6a + 4p = 14 ---- eqn 2

Let us solve eqn 1 and eqn 2 to find values of "a" and "p"

Multiply eqn 2 by 2

12a + 8p = 28 ---- eqn 3

Subtract eqn 1 from eqn 3

12a + 8p = 28

3a + 8p = 14.50

(-)----------------

9a = 13.5

a = 1.5

From eqn 1,

3a + 8p = 14.50

3(1.5) + 8p = 14.50

4.5 + 8p = 14.50

8p = 10

p = 1.25

Thus we have:

Cost of 1 apple is $ 1.5 and cost of 1 pear is $ 1.25