Question

Three times the greatest of three consecutive even integers exceeds twice the least by 38. Find the integers

Answer 1

The three numbers are 32,33, and 34.

Explanation:

Let the three consecutive integers be
`n-1,n, \text{ and } n+1` for any integer
`n`.

Integers are numbers in the set:
`\{...,-3,-2,-1,0,1,2,3,...\}`.

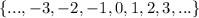We are given that '3 times greatest of these numbers exceeds 2 times the smallest of these numbers by 38'.

This means as an equation we have:

`3(n+1)=38+2(n-1)`.

Let's solve the above equation.

Distribute:

`3n+3=38+2n-2`

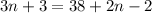
Combine like terms on the sides:

`3n+3=2n+36`

Subtract
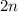`2n` on both sides:

`n+3=36`

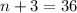
Subtract 3 on both sides:

`n=33`

Now let's find
`n-1` and
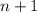`n+1` given that
`n=33`:

`n-1=33-1=32`

`n+1=33+1=34`

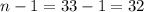
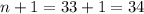
So the three numbers are 32,33, and 34.

Let's check.

3(greatest)=3(34)=102

2(least)=2(32)=64

Now let's see if 102 is 38 more than 64.

Since 38+64=102, it is.