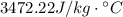Question

You then measure Polly's internal temperature to be 13°C, which is quite a drop from the normal human body temperature of 37°C. And weighing Polly, you find her mass to be 60 kg. Now, subtracting the heat warming the water from the surrounding environment, we assume Polly gave up only 5000 kJ of thermal energy to warm the bath. With these numbers, determine Polly's specific heat in units J/(kg°C)_______.

Answer 1

Using the expression to find the Heat exchange energy, we can find the required value for the Poly's specific heat in its respectively units. Matematically this can be expressed as,

`Q = mC_p \Delta T`

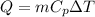
Where,

m = Mass

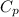`C_p`= Specific heat

`\Delta T`= Change in temperature

Q = Heat change

Re-arrange to find the specific heat we have that

`C_p = (Q)/(m\Delta T)`

`C_p = (5000*10^3)/(60(37-13))`

`C_p = 3472.22J/kg\cdot \°C`

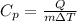
Therefore the Polly's specific heat is
`3472.22J/kg\cdot \°C`