Answer:
Standard form:
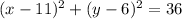
or
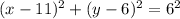
The center is
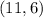 and the radius is
and the radius is
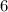 .
.
Explanation:

We will group terms with
 together and also group terms with
together and also group terms with
 together.
together.

We will not subtract 121 on both sides.
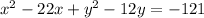
We are about to complete the square both both the
 terms and then the
terms and then the
 terms.
terms.
Whatever we add on one side, we must add to the other.
/(2))^2+(y+(-12)/(2))^2=-121+(-11)^2+(-6)^2]()
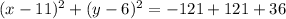
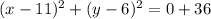
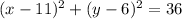
We can also write it as:
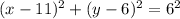
Now it it easy to compare to:

to find the center
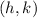 and the radius,
and the radius,
 .
.
The center is
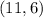 and the radius is
and the radius is
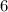 .
.