Answer:
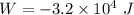
Step-by-step explanation:
Given:
Process 1:
- Volume of ideal gas is constant,

- Initial pressure,
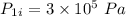
- Final pressure,
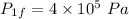
Process 2:
- Pressure of ideal gas is constant,
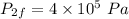
- Final volume,
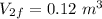
We know that the work done by an ideal gas is given as:
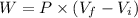
Now for process 1:
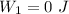
∵there is no change in volume in this process.
For process 2:
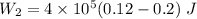
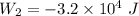
∵Negative , sign indicates that the work is being done on the gas here since the gas is being compressed.
Hence the total work done by the gas during this two step process is :


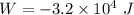 is the work done by the gas.
is the work done by the gas.