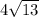Answer:
The perimeter of rhombus WXYZ is
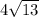
Explanation:
Step 1 :Finding length of XY
Distance formula =
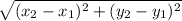
here
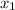 = 5
= 5
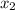 =3
=3
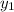 = -1
= -1
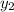 =2
=2
XY =
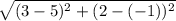
XY =
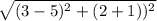
XY =
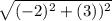
XY =

XY =
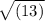
Step 2 :Finding length of YZ
Distance formula =
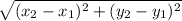
here
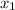 = 3
= 3
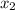 =5
=5
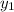 = 2
= 2
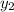 =5
=5
YZ =
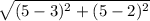
YZ =
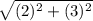
YZ =

YZ =
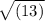
Step 3 : :Finding length of ZW
Distance formula =
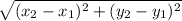
here
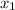 = 5
= 5
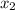 =7
=7
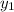 = 5
= 5
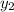 =2
=2
ZW =
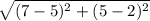
ZW =
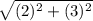
ZW =

ZW =
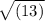
Step 4 :Finding length of WX
Distance formula =
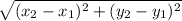
here
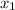 = 7
= 7
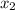 =5
=5
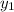 = 2
= 2
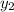 = -1
= -1
WX =
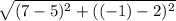
WX =
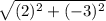
WX =

WX =
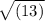
Step 5: finding the perimeter of the rhombus
Perimeter= 4 X side
=>
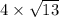
=>