Answer:
The highest height that can be reached is
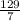 feet.
feet.
Explanation:
The height is
 .
.
Therefore, the maximum height is the
 -coordinate of the vertex.
-coordinate of the vertex.
When an equation is in standard form,
 , we can use the following formula to compute the
, we can use the following formula to compute the
 -coordinate of the vertex:
-coordinate of the vertex:
 .
.
So let's compare our equation
 to
to
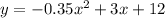 , this gives us:
, this gives us:
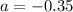
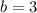
 .
.
Let's begin the
 -coordinate computation of the vertex:
-coordinate computation of the vertex:

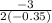
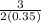
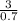
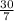 (Multiply by 10/10)
(Multiply by 10/10)
To find the corresponding
 -coordinate of the vertex given the
-coordinate of the vertex given the
 -coordinate, we just replace
-coordinate, we just replace
 in
in
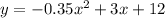 with
with
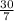 giving us:
giving us:

I will put the right hand side into my calculator:
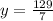
The highest height that can be reached is
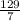 feet.
feet.