Question

2x+3y=4

and

2x-5y=-12


Solve the given system by elimination and justify each step. Which procedure would not result in a system with a pair of opposite terms?


A) Multiply both sides of 2x + 3y = 4 by −1 and use the other equation to produce a system with a pair of opposite terms. This is an application of the multiplicative property of equality.

B) Multiply both sides of 2x − 5y = −12 by −1 and use the other equation to produce a system with a pair of opposite terms. This is an application of the multiplicative property of equality.

C) Multiply both sides of 2x − 5y = −12 by 3 and multiply both sides of 2x + 3y = 4 by 5 to produce a system with a pair of opposite terms. This is an application of the multiplicative property of equality.

D) Multiply both sides of 2x − 5y = −12 by −3 and multiply both sides of 2x + 3y = 4 by 5 to produce a system with a pair of opposite terms. This is an application of the multiplicative property of equality.

Answer 1

Option D

Explanation:

we have

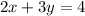`2x+3y=4` -----> equation A

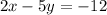`2x-5y=-12` -----> equation B

Solve the system by elimination

Multiply both sides equation A by -1

`-1(2x+3y)=-1(4)`

`-2x-3y=-4` -----> equation C

Adds equation C and equation B

`-2x-3y=-4\\2x-5y=-12\\------\\-3y-5y=-4-12\\-8y=-16\\y=2`

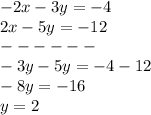
Find the value of x

substitute the value of y in either equation

`2x+3(2)=4`

`2x+6=4`

`2x=-2`

`x=-1`

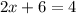
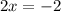
The solution is the point (-1,2)

In this problem Option A,B and C are correct

The option D not result in a system with a pair of opposite terms

because

Multiply both sides of equation B by -3

`-3(2x-5y)=-3(-12)`

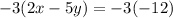
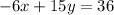`-6x+15y=36` -----> equation C

Multiply both sides of equation A by 5

`5(2x+3y)=5(4)`

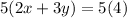
`10x+15y=20` ----> equation D

so

equation C and equation D not have a pair of opposite terms