Answer:
The growth rates at t=0, t=4 and t=8 hours are 4096, 0 and -4096 respectively.
Explanation:
Consider the provided function.

Now we need to find the growth rates at t=0, t=4 and t=8 hours.
Differentiate the above function.
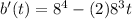
First substitute t=0 in above function.
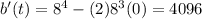
Substitute t=4 in above function.
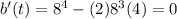
Substitute t=8 in above function.
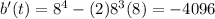
Hence, the growth rates at t=0, t=4 and t=8 hours are 4096, 0 and -4096 respectively.