Answer:
x = 9
Explanation:
Rearrange
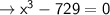
Factor using (a-b) × (a^2 +ab +b^2)
a^3 + a^2b + ab^2 - ba^2 - b^2a - b^3 =
a^3 + (a^2b-ba^2) + (ab^2-b^2a) - b^3 =
a^3 + 0 + 0 - b^3 =
a^3 - b^3
x^3 = x^1
Rearrange(Using polynomial/cube roots)
(x - 9) × (x2 + 9x + 81) = 0
Subtract/Add
x - 9 = 0 = 9
x^2 + 9x = -81
-81 + 81/4
-243/4
x^2 + 9x + (81/4) = -243/4
(x + (9/2)) × (x + (9/2)) = (x + (9/2)) × 2
(x + (9/2))2 = -243/4
x^2 + 9x + 81 = 0
√243 = 3 × 3 × 3 × 3 × 3 = 3 × 3 × √3 = ±9 × √3
= ±9x = (-9 ± 9 × 1.732(i)) / 2
= ±9x
Divide by 9 (Absolute value: positive)
|9/9| = x
Reverse, re-arranging x (Assuming x = 1)
x = |9/x|
Thus,
x = 9
Hope this helped, let me know if anything confuses you, and I will try my best to address that. Have a good day!