Question

Han and tyler both started running toward each other from opposite ends of a 10-mile path along the river. Han runs at a pace of 12 minutes per mile. Tyler runs at a pace of 15 minutes per mile. How long does it take until Han and Tyler meet?

Answer 1

The time taken by both Han and Tyler to meet at point on 10 miles path is 0.37 minutes

Explanation:

Given as :

The distance of path on which Han and Tyler run from opposite end = d = 10 miles

The speed of Han =
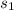`s_1` = 12 miles per min

The speed of Tyler =
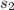`s_2` = 15 miles per min

Let The time at which both meet at a points = t minutes

Let The distance cover by Han =
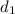`d_1` = d miles

And The distance cover by Tyler =
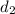`d_2` = (10-d) miles

Now, According to question

Time =
`(\textrm Distance)/(\textrm Speed)`

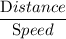
So, For Han

T =
`(d_1)/(s_1)`

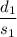
i.e T =
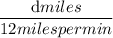`(\textrm d miles)/(\textrm 12 miles per min)` ....1

Again For Tyler

T =
`(d_2)/(s_2)`

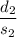
i.e T =
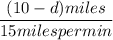`(\textrm (10-d) miles)/(\textrm 15 miles per min)` .....2

Now, Equating both equations

`(\textrm d miles)/(\textrm 12 miles per min)` =
`(\textrm (10-d) miles)/(\textrm 15 miles per min)`

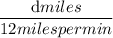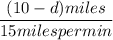
cross multiplying

15 × d = 12 × (10 - d)

Or, 15 d = 120 - 12 d

Or, 15 d + 12 d = 120

or, 27 d = 120

∴ d =
`(120)/(27)` =
`(40)/(9)`

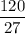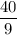
I.e d = 4.44 miles

Now, Put the value of d in eq 1

So, Time taken = T =
`(\textrm 4.44 miles)/(\textrm 12 miles per min)`

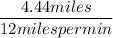
I.e T = 0.37 min

So, The time taken to meet at a point = T = 0.37 min

Hence, The time taken by both Han and Tyler to meet at point on 10 miles path is 0.37 minutes . Answer