Question

If f(x) = 2х2 +1 and g(x) = х2 -7, find (f-g)(x).

ОА. х2 + 8
ОВ. 3х2 -6
Ос. 3х2 +
OD. х2 – 6

Answer 1

Option A

If f(x) =
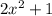`2x^2 + 1` and g(x) =
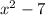`x^2 - 7` then
`(f - g)(x) = x^2 + 8`

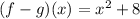
Solution:

Given that f(x) =
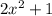`2x^2 + 1` and g(x) =
`x^2 - 7`

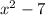
To find: (f - g)(x)

We know that,

(f – g)(x) = f (x) - g(x)

Let us substitute the given values of f(x) and g(x) in above formula,

`(f - g)(x) = 2x^2 + 1 - (x^2 - 7)`

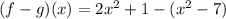
For solving the brackets in above expression,

There are two simple rules to remember:

When you multiply a negative number by a positive number then the product is always negative.

When you multiply two negative numbers or two positive numbers then the product is always positive.

So the expression becomes,

`(f - g)(x) = 2x^2 + 1 -x^2 + 7`

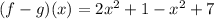
Combining the like terms,

`(f - g)(x) = 2x^2 - x^2 + 1 + 7\\\\(f - g)(x) = x^2 + 8`

Thus option A is correct