Question

Plot on graph.

Plot the axis of symmetry and the point where the maximum value occurs for the function below.

h(x)=-1/2x^2-2x+6

Answer 1

Axis of symmetry: x=-2

Maximum point: (-2,8)

Explanation:

The given function is
`h(x)=-(1)/(2)x^2-2x+6`.

We can complete the square to reveal the axis of symmetry and the vertex.

We factor to get:

`h(x)=-(1)/(2)(x^2+4x)+6`

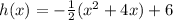
We add the zero pairs and obtain a perfect square:

`h(x)=-(1)/(2)(x^2+4x+4-4)+6`

`h(x)=-(1)/(2)(x^2+4x+4)+2+6`

`h(x)=-(1)/(2)(x+2)^2+8`

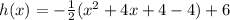
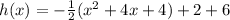
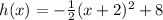
The function is now in the form
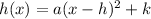`h(x)=a(x-h)^2+k`, where V(h,k) =(-2,8) is the vertex.