Answer:
The age of youngest brother is 21.
Explanation:
Given:
The ages of 3 brothers are represented by consecutive integers.
If the oldest brother's age is decreased by twice the younger brother's age, the result is -19.
Now, to find the age of youngest brother.
Let the age of youngest brother be

Let the age of middle one be
 .
.
And the age of oldest brother age be

According to question:
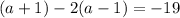
⇒
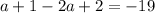
⇒
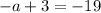
Adding
 on both sides we get:
on both sides we get:
⇒
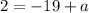
Adding 19 on both sides we get:
⇒
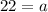
Now, getting the age of youngest brother by putting the value of
 :
:
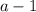
⇒
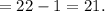
Therefore, the age of youngest brother is 21.