Question

A recent study conducted by the state government attempts to determine whether the voting public supports a further increase in cigarette taxes to help the public schools. The opinion poll recently sampled 1500 voting age citizens. 622 of the sampled citizens were in favor of an increase in taxes. The state government would like to decide if there is enough evidence to establish whether the proportion of citizens supporting an increase in cigarette taxes is significantly greater than 66%. At what level of significance will the null hypothesis not be rejected?

Answer 1

0.001%

Explanation:

Given that a recent study conducted by the state government attempts to determine whether the voting public supports a further increase in cigarette taxes to help the public schools

n = 1500

favour x = 622

Sample proportion p =
`622/1500 = 0.4147`

`H_0: p = 0.66\\H_a: p >0.66`

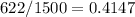
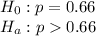
(right tailed test)

Assume H0 to be true.

Std error =
`\sqrt{(0.66*0.34)/(1500) } \\=0.01223`

p difference = -0.2453

Test statistic Z =
`(-0.2453)/(0.01223) \\=-20.05`

p value <0.00001

Hence fon ull hypothesis not to be rejected significant level should be greater than 0.00001 or 0.001%