Question

Tony saved enough money to place $125,500 in an investment generating 9.25% compounded monthly. He wants to collect a monthly income of $1,350, at the beginning of each month, for as long as the money lasts. How many months will Tony have this income coming to him?

Answer 1

It will last for 161.70 months

Step-by-step explanation:

we need to solve for n in an annuity-due

`C * (1-(1+r)^(-time) )/(rate) (1+rate)= PV\\`

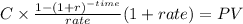
C $1,350.00

time n

rate 9.25% annual -->0.0925/ 12 = 0.007708333

PV $125,500.0000

`1350 * (1-(1+0.0077083)^(-n) )/(0.0077083) (1+0.00770833)= 125500\\`

`(1+0.0077083)^(-n)= 1-(125500*0.0077083)/(1350)(1.00770833)`

`(1+0.0077083)^(-n)= 0.29`

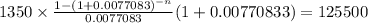
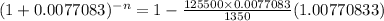
[tex]-n= \frac{log0.288891951699477}{log(1+0.0077083)

-n = -161.7057904

n = 161.7057