Question

An equation is given. (Enter your answers as a comma-separated list. Round terms to three decimal places where appropriate. If there is no solution, enter NO SOLUTION.) cos θ 2 − 1 = 0 (a) Find all solutions of the equation.

Answer 1

`\theta = n\pi`

where
`n = ..., -2,-1,0,1,2...`

Explanation:

given equation is:

`cos(2\theta) - 1 = 0`

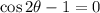
since no range is provided we can solve for all values of
`\theta`:

`cos(2\theta) = 1`

`2\theta = \cos^(-1){(1)}`

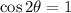
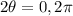`2\theta = 0, 2\pi` for one cycle of cos
`(0 \leq \theta \leq 2\pi)`

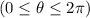
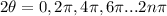`2\theta = 0, 2\pi, 4\pi, 6\pi ... 2n\pi` for all cycles of cos

we should also include negative values.

`2\theta = -4\pi,-2\pi,0, 2\pi, 4\pi,... 2n\pi`

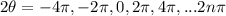
we can divide each value by 2, to get the solutions for
`\theta` instead of
`2\theta`

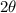
Answer:

`\theta = -2\pi,-\pi,0, \pi, 2\pi,... n\pi`

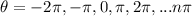
This is the solution of the equation
`cos(2\theta) - 1 = 0`.

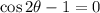In its most general form we can write all solutions of the equation in terms of
`n`

`\theta = n\pi` where
`n = ..., -2,-1,0,1,2...` or n is an integer.