Answer:
The water she need is
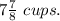 and strawberry syrup
and strawberry syrup
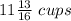 .
.
Explanation:
Given:
Dina wants to make 15 3/4 cups of strawberry drink by mixing water and strawberry syrup with a ratio of 2 1/4 cup of water for every 3/4 cup of syrup.
Now, to find the quantity of water and syrup she need to use.
As given in question ratio so:
Strawberry syrup = 2 1/4 = 9/4.
Water = 3/4.
Total cups of strawberry drink = 15 3/4 = 63/4.
Let the strawberry syrup be
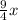 .
.
And let the water be
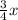 .
.
According to question:
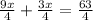 .
.
On adding the fractions:
⇒
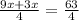
⇒
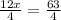
Multiplying both sides by 4 we get:
⇒
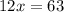
Dividing both sides by 12 we get:
⇒
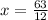
Dividing numerator and denominator by 3 on R.H.S we get:
⇒
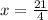
Now, putting the value of
 on ratios:
on ratios:
Strawberry syrup =
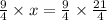
=
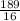
=
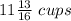
Water =
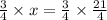
=
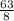
=
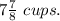
Therefore, the water she need is
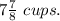 and strawberry syrup
and strawberry syrup
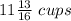 .
.