Question

Roxanne’s Farm house shelters 11 animals. Some are goats and some are ducks. Altogether There are 34 legs. How many of each animals are there

Answer 1

There are 6 goats and 5 ducks.

Explanation:

Given:

Roxanne’s farmhouse shelters 11 animals.

Some are goats and some are ducks.

Altogether there are 34 legs.

Now, to find the number of each animals are there.

Let the number of goats be
`x`.

And the number of ducks be
`y`.

So, total number of animals are:

`x+y=11`

⇒
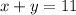
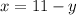`x=11-y`.......( 1 )

Now, the total number of legs:

As goats have 4 legs and ducks have 2.

`4x+2y=34`

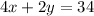
Putting the equation ( 1 ) in the place of
`x` we get:

⇒
`4(11-y)+2y=34`

⇒
`44-4y+2y=34`

⇒
`44-2y=34`

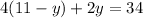
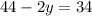
Moving variable on one side and the numbers on the other we get:

⇒
`44-34=2y`

⇒
`10=2y`

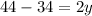
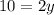
Dividing both sides by 2 we get:

⇒
`5=y`

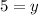
The number of ducks = 5.

Then, putting the value of
`y` in equation ( 1 ) we get:

`x=11-5`

⇒
`x=6.`

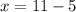
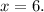
The number of goats = 6.

Therefore, there are 6 goats and 5 ducks.