Question

Cobalt-60 has a half life of 5.25 years. If you started with a 40 gram sample of pure cobalt-60, how many grams of cobalt-60 would remain after 10.5 years?

Answer 1

10 gm

Step-by-step explanation:

Given:

Cobalt-60 has a half life of 5.25 years.

Initial mass of the Cobalt = 40 grams

How much decayed after 10.5 years?

Solution:

The general equation for half life is given below.

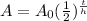`A=A_(0)((1)/(2))^{(t)/(h)}`----------(1)

Where A = mass of the substance that remains undecayed.

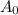`A_(0)` = the initial mass of the substance.

t = time

h = half life

Now, we substitute all known value in equation 1.

`A=40((1)/(2))^{(10.5)/(5.25)}`

`A=40((1)/(2))^(2)`

`A=40(1)/(4)`

`A=(40)/(4)`

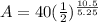
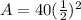
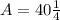
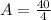
A = 10 gm

Therefore, the remaining cobalt-60 after 10.5 years is 10 gm.