Question

Derrick's Dog Sitting and Darlene's Dog Sitting are competing for new business. Derrick's Dog Sitting charges $14 plus $5 per hour. Darlene's Dog Sitting charges $18 plus $3 per hour.

54 42

Part 1 out of 2
Complete and solve the equation that can be solved to find the number of hours for which the total cost will be the same for the two services. In your equation, use x to represent the number of hours of dog sitting.


The equation is .
The total cost will be the same for the two services at hours.

Answer 1

The Equation is
`14+5x=18+3x`.

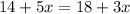The total cost will be the same for the two services at 2 hours.

Explanation:

Given:

Fixed charge of Derrick = $14

Hourly charge of Derrick = $5

Fixed charge of Darlene = $18

Hourly charge of Darlene = $3

Let number of hours be 'x'.

Hence We can say that Total Charges of Derrick's Dog Sitting will equal to sum of Fixed charge of Derrick and Hourly charge of Derrick multiplied by Number of hours.

Framing in equation form we get;

Total Charges of Derrick's Dog Sitting =
`14+5x`

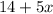
Now We can say that Total Charges of Darlene's Dog Sitting will equal to sum of Fixed charge of Darlene and Hourly charge of Darlene multiplied by Number of hours.

Framing in equation form we get;

Total Charges of Darlene's Dog Sitting =
`18+3x`

we need to find the number of hours used at which both the total cost would be same.

we can say;

Total Charges of Derrick's Dog Sitting = Total Charges of Darlene's Dog Sitting

`14+5x=18+3x`

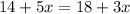
Hence the Equation is
`14+5x=18+3x`

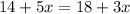
On Solving the equation we will find the numbers of hours for the same we get;

Combining like terms

`5x-3x=18-14`

`2x=4`

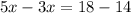
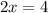
Now dividing both sides by 2 using Division property we get;

`(2x)/(2)=(4)/(2)\\\\x=2`

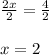
Hence, The total cost will be the same for the two services at 2 hours.