Question

What is the equation of the line which includes points HELP ASAP

Answer 1

OPTION C

OPTION A

OPTION C

Explanation:

We use two - point form to determine the equation of the line when two points are given.

The two - point form is:
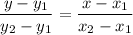`$ (y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1) $`, where
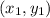`$ (x_1, y_1) $` and
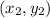`$ (x_2, y_2) $` are the two points passing through it.

1) (x₁, y₁) = (2, 3) and (x₂, y₂) = (0, 10)

Using the two - point form, we have:

`$ (y - 3)/(10 - 3) = (x - 2)/(0 - 2) $`

`$ (y - 3)/(7) = (x -2)/(-2) $`

`$ \implies - 2y + 6 = 7x - 14 $`

`$ \implies 7x - 20 = - 2y $`

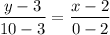
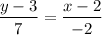
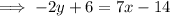
Dividing by -2, we get:

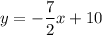`$ y = - (7)/(2)x + 10 $` is the equation of the line.

2) (x₁, y₁) = (1, 1) and (x₂, y₂) = (1, 5)

Using the slope - point form, we get:

`$ (y - 1)/(5 - 1) = (x - 1)/(1 - 1) $`

`$ \implies (y - 1)/(5 - 1) = (x - 1)/(0) $`

`$ 0 = x - 1 $`

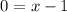
⇒ x = 1 is the required equation of the line.

3) (x₁, y₁) = (-5, 5) and (x₂, y₂) = (2, 5)

Using the slope - point form, we get:

`$ (y - 5)/(5 - 5) = (x + 5)/(2 - 5) $`

`$ \implies (y - 5)/(0) = (x + 5)/(-3) $`

`$ \implies y - 5 = 0 $`

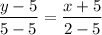
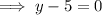
⇒ y = 5 is the required equation of the line.