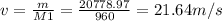Answer:
speed of car is 21.6 m/s
Step-by-step explanation:
Given speed:
sport car weight is 960 kg
SUV car weight is 2300 kg
skid distance is 2.6 m
coefficient of friction is 0.80
Taking After impact:
force of kinetic friction = µk = µ(m1 +m2) g
F = (0.80)(960+2400)(9.81) = 25,584.48 N
acceleration
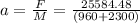
a = 7.84 m/s^2
from equation of motion
d =1/2 at^2
siolving for t
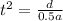
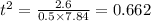
t = 0.813 s
momentum after collision MV
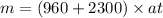
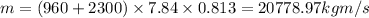
mometum of car before collision = MV = 20778.97 KGM.S
Speed of car before collision =