Question

The period of a sinusoidal source is the time required for the sinusoid to pass through all of its possible values. We use the symbol T to represent the period of a sinusoid. The period and the frequency are inversely related. A sinusoidal source described by the function cos(ωt) has a frequency of ω radians/second, or a frequency f=ω/2π Hz. The units hertz represents the number of cycles per second. Since the period is the number of seconds per cycle, the period is the inverse of the frequency in hertz: T=1f Substituting the frequency in radians/second, ω, for the frequency in Hz gives us another way to calculate the period: T=2πω What is the period of the voltage source described as v(t)=50cos(2000t−45∘) mV? Express your answer to two digits after the decimal point and include the appropriate units.

Answer 1

T=0.0031secs

Step-by-step explanation:

The voltage expression
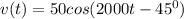`v(t)=50cos(2000t-45^(0))` can be represented as

`v(t)=v_(m)cos(wt-\alpha ) \\`

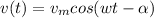
comparing the two equations we can conclude that the angular frequency

`w=2000`

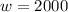
from the question, since the frequency,f which is express as

`f=(w)/(2\pi )\\`,

Hence
`f=(2000)/(2\pi ) \\f=(2000)/(2*3.14 ) \\f=318.471Hz\\`.

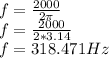The period which is the inverse of the frequency can be express as

`T=(1)/(f) \\T=(1)/(314.471)\\ T=0.00314\\T=0.0031secs`