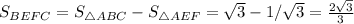Answer:

Explanation:
Since
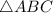 is equilateral triangle, then
is equilateral triangle, then
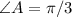
So,
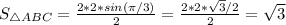
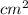
Then we need to find
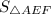 which can be computed by finding length_AF.
which can be computed by finding length_AF.
Let's call x = length_AF.
By Menelao's Theorem,
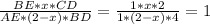
⇒ x = 4/3 cm
Thus,
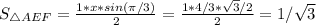
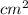
To find the area of quadrilateral
 , we have to subtract
, we have to subtract
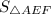 from
from
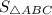
Hence,