Answer:
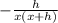
Explanation:
Given:
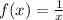
To find
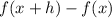
Solution.
We will first find
 by plugging in
by plugging in
 in place of
in place of
 in
in

∴

So,
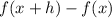
⇒
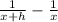
Taking LCD as product of denominators as they are unknown variables.
Making the denominators common by multiplying the with corresponding terms.
⇒
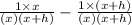
⇒

⇒
 [Subtracting the numerators]
[Subtracting the numerators]
⇒
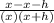
⇒
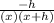
⇒
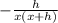 (Answer)
(Answer)