Question

In a local university, 40% of the students live in dormitories. A random sample of n = 80 students is selected for a particular study.

(a) What is the sampling distribution of P? Please provide its general shape, its standard deviation, and its mean.
(b) What is the probability that the sample proportion (the proportion living in the dormitories) is between 0.30 and 0.50?

Answer 1

a) p is normally distributed with mean P = 0.4 and standard deviation

δ = 0.05477

b) P( 0.3 < p < 0.5) = 0.9312

Explanation:

a) What is the sampling distributión of P?

p(sample proportion) is normally distributed with mean P and standard

deviation δ =
`\sqrt{(P(1-P))/(n) }`

how P = 0.40 population proportion of the students live in dormitories,

then p is normally distributed with mean P = 0.4 and standard deviation

δ =
`\sqrt{(0.4(1-0.4)/(80) }`

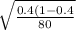
δ = 0.05477

b) P( 0.3 < p < 0.5)

Standardizing

z = (p - P)/δ

`z_(1) = (0.3-0.4)/(0.05477)`

= -1.82

`z_(2) = (0.5-0.4)/(0.05477)`

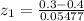
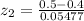
= 1.82

P(-1.82 < z < 1.82) = P(z < 1.82) - P(z<-1.82)

=0.9656 - 0.0344

P(-1.82 < z < 1.82) = 0.9312