Answer:
∆Ssys = 392.73-179.62 =213.11 J/K.
Step-by-step explanation:
m_1=145,T_1=20°C
and
m_2=235, T_2=84 °C
let, specific heat capacity be c(small)=2.42 J/g/K
let,
the constant temperature obtained after mixing is t
so heat absorbed(1st portion of ethanol),
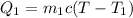
heat heat lost(2nd portion of ethanol), ,
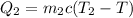
Now, heat lost= heat gained
,
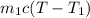 =
=
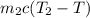
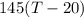 =
=
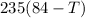
T=61.25°C
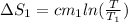
putting values we get
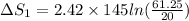
ΔS_1= 392.73 J/ K.
and
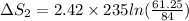
ΔS_2= -179.62557 J/K.
∆Ssys = 392.73-179.62 =213.11 J/K.