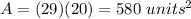Answer:
Part 1)

Part 2)
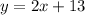
Part 3)
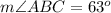
Part 4)
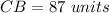
Part 5)
 ,
,
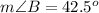 ,
,

Part 6)
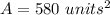
Explanation:
Part 1) Given the points (4,-2) and (8,1), what is the equation of a line that connect the two points
step 1
Find the slope
The formula to calculate the slope between two points is equal to
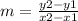
substitute the given values
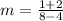
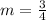
step 2
Find the equation of the line in point slope form

we have
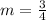
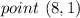
substitute
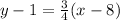
step 3
Convert to slope intercept form

isolate the variable y

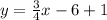

Part 2) What is the slope-intercept form of a linear equation that passes through (-3,7) and is parallel to the equation y=2x+5
we know that
If two line are parallel, then their slopes are the same
The slope of the given line is m=2
so
The slope of the line parallel to the given line is m=2
Find the equation of the line in slope intercept form

we have
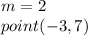
substitute
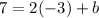
solve for b


therefore
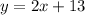
Part 3) ∠ABC is adjacent to ∠CBD. If the m∠ABC=4x+23, m∠CBD=6x+7, and m∠ABD=130°, what is the measure of angle ABC?
we know that
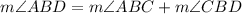 ----> by addition angle postulate
----> by addition angle postulate
substitute the given values
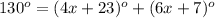
solve for x
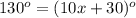

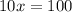
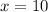
Find the measure of angle ABC
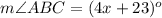
substitute the value of x

Part 4) Point B lies between the points A and C. If AC=7x+11, AB=2x+29, and CB=4x+3, what is the length of segment CB?
we know that
 -----> by addition segment postulate
-----> by addition segment postulate
Remember that
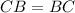
substitute the given values
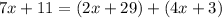
solve for x
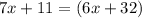
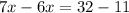
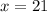
Find the length of segment CB
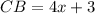
substitute the value of x
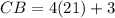
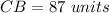
Part 5) What are the angle measures of the triangle?
we know that
An isosceles triangle has two equal sides and two equal angles
The triangle ABC of the figure is an isosceles triangle
because
AB=BC
so
∠A=∠C ----> equation A
Remember that the sum of the interior angles of triangle must be equal to 180 degrees
so
∠A+∠B+∠C=180° ----> equation B
substitute equation A in equation B
2∠A+∠B=180°
substitute the given values

solve for x
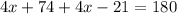
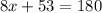
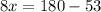


Find the angle measures of the triangle
substitute the value of x
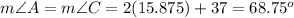
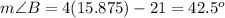
therefore

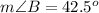

Part 6) What is the area of the rectangle?
we know that
A rectangle has opposite sides parallel and congruent
so
AB=CD
substitute the given values

solve for x

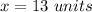
Remember that the area of rectangle is equal to

where
L is the length
W is the width
In this problem

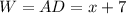
substitute the value of x
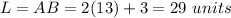
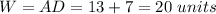
The area is equal to