Question

A polling company conducts an annual poll of adults about political opinions. The survey asked a random sample of 419 adults whether they think things in the country are going in the right direction or in the wrong direction, 54% said that things were going in the wrong direction. How many people would need to ve surveyed for a 90% confidence interval to ensure the margin or error would be less than 3%?

Answer 1

Answer: 747

Explanation:

When prior estimate of population proportion (p) is given , then the formula to find the sample size is given by :-

`n=p(1-p)((z^*)/(E))^2`

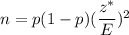
, where z* = Critical value and E = Margin of error.

As per given , we have

p= 0.54

E= 0.03

Critical value for 90% confidence : z* = 1.645

Then, the required sample size is given by :-

`n=0.54(1-0.54)((1.645)/(0.03))^2`

`n=0.2484(54.8333333333)^2`

`n=746.862899999\approx747`

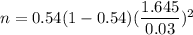
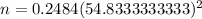
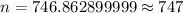
Hence, the number of people would be needed = 747