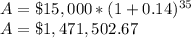Answer:
A. $115,291.30
B. $421,536.55
C. $1,471,502.67
Step-by-step explanation:
The expression that describes the final amount of a $15,000 investment compounded annually for 35 years is:
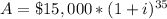
A. 6% per year
i = 0.06
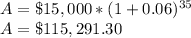
B. 10% per year
i = 0.10
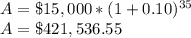
C. 14% per year
i = 0.14