Answer:
Tickets were sold in advance are 60 and the tickets were sold at the door are 40.
Explanation:
Given:
Tickets for a high school dance.
Cost $1.00 each of purchased in advance of the dance.
Cost $1.50 each if bought at the door.
100 tickets were sold and $120 was collected.
Now, to find the tickets that were sold in advance and sold at the door.
Let the number of tickets sold in advance be
 .
.
And the number of tickets sold at the door be
 .
.
So, the total number of tickets sold:
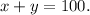
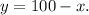 ......(1)
......(1)
Now, the total amount collected:
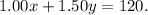
Putting the equation (1) in the place of
 we get:
we get:
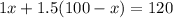
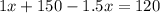
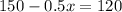
Adding both sides by
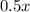 we get:
we get:
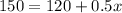
Subtracting both sides by 120 we get:
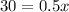
Dividing 0.5 by both sides we get:
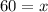
Thus, the number of tickets sold in advance = 60.
Putting the value of
 in equation (1) we get:
in equation (1) we get:
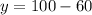
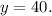
So, the number of tickets sold at the door = 40.
Therefore, tickets were sold in advance are 60 and tickets were sold at the door are 40.