Question

A random sample of 11fields of spring wheat has a mean yield of 20.2bushels per acre and standard deviation of 5.19 bushels per acre. Determine the 99% confidence interval for the true mean yield. Assume the population is approximately normal.Step 1 of 2:Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.Step 2 of 2:Construct the 99% confidence interval. Round your answer to one decimal place

Answer 1

1.
`t_(0.01/2,(10))=3.169`

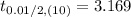
2. Confidence interval = [15.2, 25.2]

Explanation:

X = 20.2

S = 5.19

n = 11

Step 1 of 2: Critical value

α = 1 - 0.99 = 0.01

df = 11 - 1 = 10

Looking at t distribution table with α = 0.01 and df = 10, we find

`t_(0.01/2,(10))=3.169`

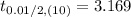
Step 2 of 2: 99% confidence interval

`std-err=(S)/(√(n))=(5.19)/(√(11))=1.5648`

`X+t_(0.01/2,10)*std-err`

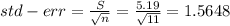
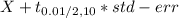
20.2 + 3.169*1.5648

20.2 + 4.9595

25.2

`X-t_(0.01/2,10)*std-err`

20.2 - 3.169*1.5648

20.2 - 4.9595

15.2

Confidence interval = [15.2, 25.2]

Hope this helps!