Answer:
323.15 °C
Step-by-step explanation:
Considering the ideal gas equation as:
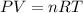
where,
P is the pressure
V is the volume
n is the number of moles
T is the temperature
R is Gas constant having value = 0.0821 L.atm/K.mol
Thus, at constant volume and number of moles, Pressure of the gas is directly proportional to the temperature of the gas.
P ∝ T
Also,
Using Charle's law
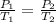
Given ,
P₂ = 2P₁
T₁ = 25 °C
T₂ = ?
The conversion of T( °C) to T(K) is shown below:
T(K) = T( °C) + 273.15
So,
T₁ = (25 + 273.15) K = 298.15 K
Using above equation as:
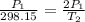

New temperature = 596.3 K
Also,
T(K) - 273.15 = T( °C)
So, Temperature = 596.3 - 273.15 °C = 323.15 °C