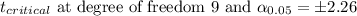Question

The data below refers to the time in hours spent on mobile internet by sample of 10 students in a class. 39 42 47 45 32 45 37 34 33 29 Assume that the population data follows a normal distribution with unknown mean and unknown standard deviation. Find a 95% confidence interval estimate of μ . [33.813, 42.787] hours [35.557, 41.936] hours [34.664, 41.936] hours

Answer 1

Option A) (33.813,42.787)

Explanation:

We are given the following data set:

39, 42, 47, 45, 32, 45, 37, 34, 33, 29

Sample size, n = 10

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(383)/(10) = 38.3`

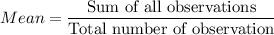
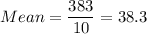
Sum of squares of differences = 354.1

`S.D = \sqrt{(354.1)/(9)} = 6.27`

95% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

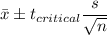
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 9 and}~\alpha_(0.05) = \pm 2.26`

`38.3 \pm 2.262((6.27)/(√(10)) ) = 38.3\pm 4.484= (33.813,42.787)`