Question

If the sides of a square are increased by 3 inches, the area becomes 64

square inches. Determine the length of the sides of the original square.

Answer 1

`Length\ of\ the\ side=5\ inches`

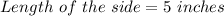
Explanation:

Let x be the length of the sides of the original square.

Given:

The sides of a square are increased by 3 inches, the area becomes 64

So, the length of the side
`x+3`

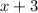
The area of the square is

`Area=(length\ of\ the\ side)^(2)`

`Area=(x+3)^(2)`

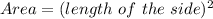
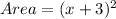
Substitute area value in above equation.

`64=(x+3)^(2)`

`(x+3)=(64)^{(1)/(2)}`

`x+3=√(64)`

`x+3=\sqrt{8^(2)}`

`x+3=8`

`x=8-3`

`x=5\ inches`

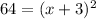
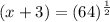
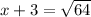
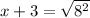
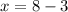
Therefore, the length of the sides of the original square is 5 inches.