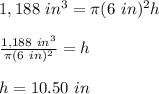1 Answer

Adamyonk · Answer 1 · 2020-03-26T02:23:10+0000

Answer:
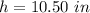
$h=10.50\ in$

Explanation:

As the information given in the exercise indicates, the formula that is used to calculate the volume of a cylinder is:

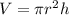
$V=\pi r^2h$

Where "r" is the radius and "h" is the height.

You know that the volume of the can is:

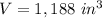
$V=1,188\ in^3$

And the radius of the base of the can must be the following:

$r=6\ in$

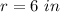
Then, the next step is to subsitute these values into the formula:

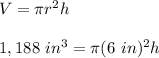
$V=\pi r^2h\\\\1,188\ in^3=\pi (6\ in)^2h$

Finally, you must solve for "h", in order to calculate the height that the can must have to get a radius of 6 inches.

Therefore, this is:

$1,188\ in^3=\pi (6\ in)^2h\\\\(1,188\ in^3)/(\pi (6\ in)^2)=h\\\\h=10.50\ in$

Please log in or register to add a comment.