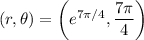Question

You are given the polar curve r = e^θ

List all of the points (r,θ) where the tangent line is horizontal. In entering your answer, list the points starting with the smallest value of r and limit yourself to 1<_r<_1000 ( note the restriction on r) and 0≤θ<2????. If two or more points share the same value of r, list those starting with the smallest value of θ. If any blanks are unused, type an upper-case "N" in them.
Point 1: (r, θ) = ________
Point 2: (r, θ) = ________
Point 3: (r, θ) = ________

Answer 1

The tangent to
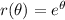`r(\theta)=e^\theta` has slope
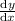`(\mathrm dy)/(\mathrm dx)`, where

`\begin{cases}x(\theta)=r(\theta)\cos\theta\\y(\theta)=r(\theta)=\sin\theta\end{cases}`

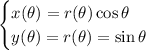
By the chain rule, we have

`(\mathrm dy)/(\mathrm dx)=((\mathrm dy)/(\mathrm d\theta))/((\mathrm dx)/(\mathrm d\theta))`

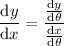
and by the product rule,

`(\mathrm dx)/(\mathrm d\theta)=(\mathrm dr)/(\mathrm d\theta)\cos\theta-r(\theta)\sin\theta`

`(\mathrm dy)/(\mathrm d\theta)=(\mathrm dr)/(\mathrm d\theta)\sin\theta+r(\theta)\cos\theta`

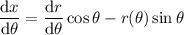
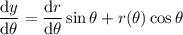
so that with
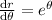`(\mathrm dr)/(\mathrm d\theta)=e^\theta`, we get

`(\mathrm dy)/(\mathrm dx)=(e^\theta\sin\theta+e^\theta\cos\theta)/(e^\theta\cos\theta-e^\theta\sin\theta)=(\sin\theta+\cos\theta)/(\cos\theta-\sin\theta)=-(1+\sin(2\theta))/(\cos(2\theta))`

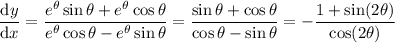
The tangent line is horizontal when the slope is 0; this happens for

`-(1+\sin(2\theta))/(\cos(2\theta))=0\implies\sin(2\theta)=-1\implies2\theta=-\frac\pi2+2n\pi\implies\theta=-\frac\pi4+n\pi`

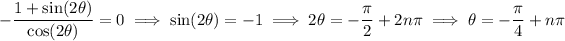
where
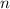`n` is any integer. In the interval
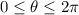`0\le\theta\le2\pi`, this happens for
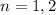`n=1,2`, or

`\theta=\frac{3\pi}4\text{ and }\theta=\frac{7\pi}4`

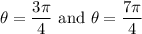
i.e at the points

`(r,\theta)=\left(e^(3\pi/4),\frac{3\pi}4\right)`

and

`(r,\theta)=\left(e^(7\pi/4),\frac{7\pi}4\right)`